Suppose that mortality follows deMoivre’s law with limiting age \(w=100\). Let \(i=6\%\) and \(x=35\). Then,
\begin{eqnarray*}
\bar{A}_{35} = \int_0^{65} v^t ~_t p_{35} \mu_{35+t}~ dt = \frac{1}{65} \int_0^{65} v^t dt = \frac{1}{65} \bar{a}_{\overline{65}|}
\end{eqnarray*}
and
\begin{eqnarray*}
P^n = \frac{\bar{A}_{35}}{\bar{a}_{35}} =\frac{\delta \bar{A}_{35}}{1-\bar{A}_{35}} =
\frac{\delta \bar{a}_{\overline{65}|} /65}{1-\bar{a}_{\overline{65}|} /65} = 0.020266.
\end{eqnarray*}
Similarly, we have \(\bar{A}_{35+t}=\bar{a}_{\overline{65-t}|}/(65-t)\) and
\begin{eqnarray*}
\bar{a}_{35+t}= \frac{1-\bar{A}_{35+t}}{\delta} =\frac{1-\bar{a}_{\overline{65-t}|}/(65-t)}{\delta}
\end{eqnarray*}
The policy value may be written as
\begin{eqnarray*}
_t V^n = \frac{\bar{a}_{\overline{65-t}|}}{65-t} – (0.020266)\frac{65-t-\bar{a}_{\overline{65-t}|}}{\delta(65-t)}.
\end{eqnarray*}
and its associated variability is
\begin{eqnarray*}
\textrm{Var}(L_t^n|T>t)&=& \left(1+\frac{0.020266}{\delta}\right)^2 \left( \frac{~^2 \bar{a}_{\overline{65-t}|}}{65-t} – \left[\frac{\bar{a}_{\overline{65-t}|}}{65-t}\right]^2 \right) \\
&=&
1.813821 \left( \frac{~^2 \bar{a}_{\overline{65-t}|}}{65-t} – \left[\frac{\bar{a}_{\overline{65-t}|}}{65-t}\right]^2 \right)
\end{eqnarray*}
using \(\delta = \ln(1.06)\).
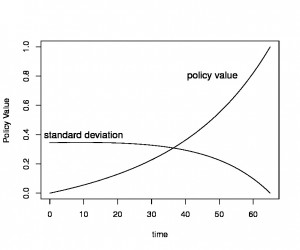
Figure 2 summarizes these calculations. Note that the policy value is 0 at \(t=0\). At \(t=65\), the policy value becomes 1. Also at \(t=65\), there is no uncertainty about the value of the policy and so the standard deviation becomes 0.